Procedurally Generated Pirate Map

Back in January reddit user Bergasms organized a friendly challenge in the procedural generation subreddit. The goal of this challenge was to procedurally generate a pirate map. I participated and ended up with some pretty nice results. I mostly used the challenge as an oppurtunity to try some interesting algorithms I had heard of but never implemented or used myself.

General approach

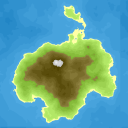
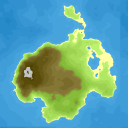
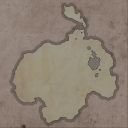
First a heightmap is generated to determine the shape of the main landmass, then another heightmap is generated to determine the actual height of that landmass, that height then directly translates to the type of terrain that will appear on that landmass. Depending on the height the map is divided into 'sea', 'land', 'inland lakes (sea level)', 'forested land' and 'mountains'. The background for the sea has a different color than the background of the landmass. The sea is decorated using some varying wave images. The inland lakes are indicated by overlaying some diagonal lines and an outline. The forests are indicated by some small trees. The mountains are decorated by placing multiple mountain images close together in a specific pattern. An 'x' with a dashed line is rendered over top to indicate where the pirate's treasure lies. Mountains are given names and finally a random compass rose is rendered.

Heightmaps

The two heightmaps are generated using the diamond-square algorithm. In the default algorithm the random distribution is uniform, however I was seeking specifically to generate the shape of an island, so instead of using a totally random number distribution I make sure the random number generator returns low values at the edges of the heightmap and a high value in the center of the map. This ensures that the generated landmass will be centrally located and surrounded by water. The shape of the landmass is then determined by a fixed threshold. As a final touch the entire heightmap is translated so that the landmass is centered.

Because we used this non-uniform random distribution we will always end up with a peak in the middle of the heightmap. This means it cannot be used directly to determine the height of the terrain on the island itself (because we would always end up with a very similar looking mountain in the middle of the island). So, in order to generate terrain on the landmass, another heightmap is generated (this time with an unmodified random number distribution).

In order to get our final terrain heightmap we combine both the 'landmass' and 'terrain' heightmaps. The combined heightmap will mostly use the sea portion of the 'landmass' heightmap and the land portion of the 'terrain' heightmap. But at the transition between the two they will be interpolated so the height change at the island's shores will be slightly less drastic. The resulting heightmap is then smoothed using a gaussian filter three times.

Background selection

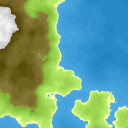
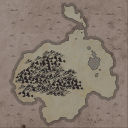
Now that we have these heightmaps, we can generate the background color image. This is a relatively straightforward process. We use simple threshold values on the 'landmass' heightmap to determine whether a pixel is supposed to be land (height >= 0.5) or sea (height < 0.5). Additionaly if a pixel is classified as land and its height in the combined heightmap satisfies (height < 0.5) it will be an inland lake. According to this classification we sample from different textures (shown below).

Isolines around the landmass

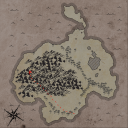
The lines around the island are created by first creating a distance field (indicating the distance from the shore). Then to get each isoline a thresholded image is created (using an increasingly large distance from the shore as the threshold). On these thresholded images an edge detection algorithm is run, the combined results of these edge detection are then rendered on top of the background.

Placing Decorations

Decoration placement is done by generating several lists of points in a poisson-disc disribution . For each of the decorations the size of the decoration is used to determine the spacing between the points). For each of the points a decoration appropriate (depending on the height in the combined heightmap) for the location on the map is randomly selected from a few possibilities.

Naming of features

A connected component analysis is used to determine individual mountain 'ranges'. The size of the components (in number of pixels) determines the descriptor used to describe it, these are 'Hill', 'Mountain', 'Range' and 'Massive'.

Results

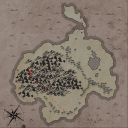
The code for the competition was written in C. You can try out the live demo which was created by using emscripten to compile the C code. In order to get a new map you simply have to refresh the page.

References

[1] procedural generation subreddit
[2] diamond-square algorithm
[3] poisson-disc disribution
[4] live demo